Gerak Rotasi Suatu Benda Pada Katrol Fisika

Gerak Rotasi Sebuah Benda dan Tali Pada Katrol
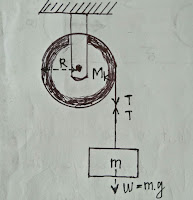
Sebuah benda yang digantung dan dihubungkan dengan seutas tali pada katrol tetap. Mula-mula benda diam dan kemudian dilepaskan, maka akan bergerak turun ke bawah searah gerak benda. Berat benda (w) bergerak turun ke bawah menyebabkan momen gaya (torsi) pada katrol dan berputar atau gerak rotasi.

Sesuai Hukum II Newton, gerak translasi atau gerak lurus pada sistem dapat dirumuskan menjadi:

           EF = m.a

   m.g - T = m.a

             T = m.g - m.a

T adalah tegangan tali yang antara katrol dan benda. m adalah massa benda yang dihubungkan katrol.

Sedangkan Hukum II Newton pada katrol yang berputar atau gerak rotasi, maka momen gaya (t) yang berpengaruh pada gerak rotasi katrol dan momen inersia (I) pada katrol yang dianggap sebagai benda berbentuk silinder pejal/padat (momen inersia I=½Mk.R²).

        Et = I.α

      T.R = ½.Mk.R². a/R

         T = ½.Mk. a

T adalah tegangan tali yang antara katrol dan benda. Mk adalah massa katrol yang berputar/rotasi.

Kedua gerak tersebut berlaku pada sistem secara bersamaan dengan tegangan tali (T) yang besar nilai sama, sehingga dapat digabung dan dirumuskan menjadi:

            T rotasi = T translasi

            ½.Mk. a = m.g - m.a

 ½.Mk. a + m.a = m.g

    (m+½.Mk) a = m.g

                       a = m.g / (m+½.Mk)

Maka rumus untuk menghitung:

• Percepatan benda bergerak yang dihubungkan tali pada katrol adalah a = m.g / (m+½.Mk).
• Percepatan sudut katrol saat berputar adalah α = a/R.
• Tegangan tali yang menghubungkan benda dan katrol dapat menggunakan rumus (T = m.g - m.a) atau (T = ½.Mk. a).
• Jarak atau ketinggian yang ditempuh benda yang digantung pada katrol setelah t detik dari saat dilepaskan adalah h = ½.a.t².
• Waktu yang diperlukan untuk menempuh jarak h meter dari saat dilepaskan adalah t = √2h/a.
• Kecepatan benda (v) tersebut setelah bergerak selama t detik dari saat dilepaskan adalah v = a.t.

Soal dan penyelesaian gerak rotasi pada katrol.

1. Sebuah ember bermassa 20 kg digantung dan dihubungkan dengan seutas tali pada sebuah katrol yang berbentuk silinder pejal bermassa 10 kg. Mula-mula ember ditahan dan kondisi diam kemudian dilepaskan. Jika jari-jari 25 cm dan percepatan gravitasi Bumi g = 10 m/s².  Tentukan:

a. percepatan gerak benda saat bergerak turun,

b. percepatan sudut katrol saat berputar,

c. tegangan tali,

d. jarak yang ditempuh benda saat turun ke bawah setelah ½ detik!
Penyelesaian:
Diketahui: m   = 20 kg
                    Mk = 10 kg
                    R    = 25 cm = 0,25 m
                    g     = 10 m/s²
Jawab:
a. Percepatan benda bergerak adalah
      a = m.g / (m+½.Mk)
         = 20.10 / (20+½.10)
         = 200 / 25
         = 8 m/s²
b. Percepatan sudut katrol saat berputar adalah
      α = a/R = 8/0,25 = 32 rad/s²
c. Tegangan tali sebesar:
      T = m.g - m.a
         = 20.10 - 20.8 = 200 - 160 = 40 N
       atau
      T = ½.Mk. a
          = ½.10.8 = 40 N
d. Jarak atau ketinggian yang ditempuh setelah t = ½ detik dari saat dilepaskan adalah
        h = ½.a.t² = ½.8.(½)² = 1 m.

2. Sebuah katrol memiliki jari-jari 50 cm  dan bermassa 1 kg berbentuk silinder pejal homogen dililiti tali dan pada ujung tali digantungkan beban 2 kg, sehingga katrol berputar setelah dilepaskan. Besar tegangan tali sebesar ...
Penyelesaian:
Diketahui: m   = 2 kg
                    Mk = 1 kg
                    R    = 50 cm = 0,5 m
                     g    = 10 m/s²
Jawab:
a. Percepatan benda bergerak adalah
      a = m.g / (m+½.Mk)
         = 2.10 / (2+½.1)
         = 20 / 2,5
         = 8 m/s²
b. Percepatan sudut katrol saat berputar adalah
      α = a/R = 8/0,5 = 16 rad/s²
c. Tegangan tali sebesar:
      T = m.g - m.a
         = 2.10 - 2.8 = 20 - 16 = 4 N
       atau
      T = ½.Mk. a

          = ½.1.8 = 4 N

3. Sebuah katrol memiliki jari-jari 10 cm  dan dililiti tali dan pada ujung tali digantungkan beban 0,4 kg, sehingga katrol berputar setelah dilepaskan. Jika momen inersia 4 x 10^-3 kg.m²,  maka besar tegangan tali sebesar ...
Penyelesaian:
Diketahui: m   = 0,4 kg
                    I     = 4 x 10^-3 = 0,004
                    R    = 10 cm = 0,1 m
                    g    = 10 m/s²
Jawab:
             T = m.g - m.a
dan

                        T.R = I.α
       (m.g - m.a) R = I . a/R
      (m.g -m.a) R² = I . a
   m.g.R² - m.a.R² = I . a
                  m.g.R² = (I + m.R²). a
 (m.g.R²)/ (I + m.R²) = a
atau
a = (m.g.R²)/ (I + m.R²)
a = (0,4 . 10 . 0,1²)/(0,004 + 0,4 . 0.1²)
a = (0,04)/(0,008) = 5 m/s²
Menentukan tegangan tali dengan rumus:
T = m.g - m.a
T = 0,4 . 10 - 0,4 . 5 = 4 - 2 = 2 N

Gerak Rotasi Dua Benda dan Tali Pada Katrol

Dua benda bermassa m1 dan m2 yang dihubungkan dengan seutas tali dan dililitkan pada sebuah katrol yang berjari-jari R. Mula-mula kedua benda ditahan dalam kondisi diam, selanjutnya dilepaskan dan menyebabkan katrol berputar atau berotasi.

Jika massa benda m2 lebih besar dari massa benda m1, maka gerak kedua benda searah dengan gerak benda bermassa yang lebih besar atau m2. Sistem seperti ini biasa dikenal dengan nama pesawat Atwood dengan menggunakan katrol berbentuk silinder atau dianggap sebagai silinder pejal. Katrol yang digunakan bermassa Mk dan berjari-jari R.
Pada benda bermassa lebih besar (m2) berlaku Hukum II Newton:
                EF = m2.a
        w2 - T2 = m2.a
     m2.g - T2 = m2.a
                 T2 = m2.g - m2.a
(T2 adalah tegangan tali pada massa yang besar).
Pada benda bermassa lebih kecil (m1) berlaku Hukum II Newton:
                EF = m1.a
        T1 - w1 = m1.a
     T1 - m1.g = m1.a
                 T1 = m1.g + m1.a
T1 adalah tegangan tali pada massa yang kecil).
Pada katrol berlaku momen gaya atau torsi berlaku:
                   Et = I.α
    T2.R - T1.R = I.α
Karena katrol dianggap silinder pejal maka momen inersia I = ½.Mk.R²  dan α = a/R, sehingga diperoleh:
   T2.R - T1.R = ½.Mk.R² . a/R
    (T2 - T1).R = ½.Mk.R² . a/R
           T2 - T1= ½.Mk . a
Selanjutnya T2 dan T1 diganti menjadi:
   (m2.g - m2.a) - (m1.g + m1.a) = ½.Mk.a
m2.g - m2.a - m1.g - m1.a = ½.Mk.a
m2.g - m1.g = ½.Mk.a + m2.a + m1.a
m2.g - m1.g = (½.Mk + m2 + m1). a
maka diperoleh:
(m2.g - m1.g) / (½.Mk + m2 + m1) = a
                      atau
a = (m2.g - m1.g) / (½.Mk + m2 + m1)
(a adalah percepatan gerak sistem tersebut).

Maka rumus untuk menghitung dua benda yang digantungkan pada sebuah katrol:

• Percepatan sistem dua benda bergerak yang dihubungkan tali pada katrol adalah  a = (m2.g - m1.g) / (½.Mk + m2 + m1)
• Percepatan sudut katrol sistem tersebut saat berputar adalah α = a/R.
• Tegangan tali yang menghubungkan kedua benda dan katrol yang meliputi teganan tali T1 dan T2 dapat menggunakan rumus yaitu T1 = m1.g + m1.a dan T2 = m2.g - m2.a
• Jarak atau ketinggian yang ditempuh kedua benda yang digantung pada katrol setelah t detik dari saat dilepaskan adalah h = ½.a.t².
• Waktu yang diperlukan untuk menempuh jarak h meter dari saat dilepaskan hingga kedua benda menempuh h meter adalah t = √2h/a.
• Kecepatan kedua benda (v) tersebut setelah bergerak selama t detik dari saat dilepaskan adalah v = a.t.
• Kecepatan sudut putar katrol tersebut setelah bergerak selama t detik dari saat dilepaskan adalah omega w = α.t.

Contoh soal dan penyelesaian:
1. Sebuah pesawat Atwood terdiri dari katrol yang dianggap sebagai silinder pejal dan bermassa 4 kg digantung dua benda bermassa 5 kg dan 3 kg. Jika percepatan gravitasi dianggap 10 m/s² dan katrol berjari-jari 50 cm, tentukan percepatan kedua benda, percepatan sudut katrol, dan tegangan kedua tali ?
Penyelesaian:
      Mk = 4 kg
      m1 = 3 kg
      m2 = 5 kg
      R    = 50 cm = 0,5 m
      g    = 10 m/s²
a. Percepatan kedua benda sebesar:
     a = (m2.g - m1.g) / (½.Mk + m2 + m1)
     a = (5.10 - 3.10) / (½.4 + 5 + 3 )
     a = (50 - 30) / (10) = 20/10
     a = 2 m/s²
b. Percepatan sudut putar katrol sebesat:
     α = a/R = 2/0,5 = 4 rad/s²
c. Tegangan tali yang menghubungkan katrol dan massa m1 adalah
    T1 = m1.g + m1.a
    T1 = 3.10 + 3.2
    T1 = 30 + 6 =36 N.
dan tegangan tali yang menghubungkan katrol dan massa m2 adalah
    T2 = m2.g - m2.a
    T2 = 5.10 - 5.2
    T2 = 50 -10 = 40 N.
Jadi besar tegangan tali sebesar 40 N dan 30 N.

2. Dua benda masing-masing memiliki massa m1 = 2 kg dan m2 = 4 kg dihubungkan dengan katrol bermassa 4 kg. Jika percepatan gravitasi g = 10 m/s², maka percepatan yang dialami adalah ...
Penyelesaian:
      Mk = 4 kg
      m1 = 2 kg
      m2 = 4 kg
      g    = 10 m/s²
Percepatan kedua benda sebesar:
     a = (m2.g - m1.g) / (½.Mk + m2 + m1)
     a = (4.10 - 2.10) / (½.4 + 4 + 2 )
     a = (40 - 20) / (8) = 20/8
     a = 2,5 m/s²

3. Sebuah roda katrol homogen yang pejal memiliki massa 2 kg dan diameter 20 cm. Katrol digantungi dua benda bermassa 2 kg dan 1,5 kg yang dihubungkan dengan seutas tali. Massa tali diabaikan dan percepatan gravitasi 10 m/s². Mula-mula katrol dalam keadaan diam, kemudian kedua benda dilepaskan dan bergerak sehingga katrol ikut berputar. Setelah 36 detik berputar, katrol memiliki energi kinetik sebesar ... Joule
Penyelesaian:
      Mk = 2 kg
      m1 = 1,5 kg
      m2 = 2 kg
      g    = 10 m/s²
      d    = 20 cm  R = 10 cm = 0,1 m
Percepatan kedua benda sebesar:
     a = (m2.g - m1.g) / (½.Mk + m2 + m1)
     a = (2.10 - 1,5.10) / (½.2 + 2 + 1,5 )
     a = (20 - 15) / (4,5) = 5/4,5
     a = 5/4,5 m/s²
Percepatan sudut putar katrol sebesar:
     α = a/R = (5/4,5)/0,1 = 5/0,45 rad/s²
Energi kinetik katrol berputar sebesar:
     E = ½.I.w² = ½.(½.Mk.R²).(α.t)²
     E = ½.(½.Mk.R²).(α.t)²
     E = ½.(½.2.(0,1)²).(5/4,5)².(36)²
     E = 800 Joule.

Sumber:

1. Rufaida, Sufi Ani. 2013. Cara Jitu Menghadapi UN Fisika Untuk SMA/MA. Surakarta: Mediatama..

2. Urip Widodo, dkk. Fisika untuk SMA/MA Kelas XIb. Sagufindo Kinarya.
3. Ketut Lasmi. 2004. Bimbingan Pemantapan Fisika untuk SMA. Bandung: Yrama Widya.
4. Tim Permata. 2016. Fisika Peminatan Ilmu Alam Untuk SMA/MA Kelas XI Semester 1. Surakarta: Cahaya Pustaka.
5. Risdiyani Chasanah, Dhara Nurani, dan Adip Ma'rufu Sururi. 2017. Fisika untuk SMA/MA Kelas XI. Klaten: Intan Pariwara.