FISIKA MATERI VEKTOR
Memahami dan Mengaplikasikan Materi Vektor
Materi vektor merupakan materi yang sulit dipahami oleh siswa jika tidak dijelaskan materi matematika trigonometri terlebih dahulu. Materi trigonometri terkait dengan notasi sin 𝞪, cos 𝞪, dan tan 𝞪 yang sangat terkait dalam penjabaran vektor pada koordinat Cartesius pada arah sumbu x dan sumbu y. Agar lebih cepat dipahami siswa, sebaiknya siswa dijelaskan konsep sin 𝞪 dan cos 𝞪.
Jika siswa sudah memahami konsep mata, maka kita mengubah konsep tersebut dengan mengganti mata menjadi 𝞪 (alpha), 𝞫 (beta), 𝞬 (gamma) atau simbol lain.
Jadi sisi di depan mata atau simbol dinamakan depan.
sisi yang menghadap sudut siku-siku dinamakan miring
sisi antara mata atau simbol dengan sudut siku-siku dinamakan samping
Kemudian dijelaskan konsep trigonometri tentang sin 𝞪, cos 𝞪, dan tan 𝞪.






 Untuk lebih mudah menghafal biasanya disingkat dalam pembacaannya misalnya sindemi, cossami, dan tandesa. Selanjutnya dijelaskan bahwa depan dianggap y, samping danggap x, dan miring dianggap r.
Untuk lebih mudah menghafal biasanya disingkat dalam pembacaannya misalnya sindemi, cossami, dan tandesa. Selanjutnya dijelaskan bahwa depan dianggap y, samping danggap x, dan miring dianggap r.
Kemudian siswa dijelaskan dan diberi contoh dengan cara memberi nilai pada setiap variabel baik x, y, dan r.
Jika dinyatakan dalam bentuk sin 𝛂, cos 𝛂, dan tan 𝛂 diperoleh:



Pada materi vektor, sisi miring r dianggap sebagai vektor utama. Jika r mewakili dari vektor gaya, maka ditulis dengan notasi "F", jika r mewakili dari vektor kecepatan, maka ditulis dengan notasi "v", dan sesuai dengan besaran yang diwakilinya.
Tanda garis miring // menunjukkan panjang bagian/sisi atas atau bawah arah horisontal yaitu x memiliki panjang yang sama. Besar panjang x dari rumus cos 𝛂 dan merupakan komponen vektor yang searah sumbu x adalah:
x = r. cos 𝛂
Tanda garis miring /// menunjukkan panjang bagian/sisi kiri atau kanan arah vertikal yaitu y memiliki panjang yang sama. Besar panjang y dari rumus sin 𝛂 dan merupakan komponen vektor yang searah sumbu y adalah:
y = r. sin 𝛂
1. Sebuah Gaya yang Bekerja di Bidang Koordinat Cartesius
1.a. Penguraian Sebuah Gaya di Koordinat Cartesius Kuadran 1
Sebuah vektor gaya yang bekerja pada kuadran 1 menghasilkan penguraian gaya yaitu searah sumbu x positif sebesar Fx = F. Cos 𝛉 dan searah sumbu y positif sebesar Fy = F. Sin 𝛉.
Misalnya gaya yang bekerja sebesar 10 N dengan sudut sebesar 30⁰ , maka
Fx = F. Cos 𝛉 = 10. Cos 30⁰ = 10. 1/2 = 5
= 5 N
N
Fy = F. Sin 𝛉 = 10. Sin 30⁰ = 10. 1/2= 5 N
1.b. Penguraian Sebuah Gaya di Koordinat Cartesius Kuadran 2
Sebuah vektor gaya yang bekerja pada kuadran 2 menghasilkan penguraian gaya yaitu searah sumbu x negatif sebesar Fx = F. Cos 𝛉 dan searah sumbu y positif sebesar Fy = F. Sin 𝛉.
Misalnya gaya yang bekerja sebesar 40 N dengan sudut sebesar 30⁰ , maka
Fx = F. Cos 𝛉 = 40. Cos 30⁰ = 40. 1/2 = 20
= 20 N
N
1.e. Penguraian Gaya di Koordinat Cartesius dengan Sudut antara Vektor dan Sumbu Y

SOAL DAN PEMBAHASAN/PENYELESAIAN
1. Perhatikan vektor gaya di bawah ini!
Jika nilai F = 2 N, nilai komponen vektor pada sumbu x dan sumbu y yang tepat adalah ...
a. Fx = 1 N d. Fx = -1 N
Fy = N Fy = -
N Fy = - N
N
b. Fx = 1 N e. Fx = N
N
Fy = - N Fy = -1 N
N Fy = -1 N
c. Fx = N
N
Fy = 1 N
 .
.
Sudut apit kedua vektor tersebut adalah....
a. 60⁰
b. 30⁰
c. 150⁰
d. 120⁰
e. 45⁰
Pembahasan:
5. Gaya-gaya berikut bekerja pada suatu benda: 7 N ke utara, 20 N berarah 37 dari timur, dan 4 N ke barat. Besar resultan ketiganya adalah.... (sin 37 = 0,6)
a. 5 N
b. 10 N
c. 13 N
d. 22,5 N
e. 25 N
Pembahasan:
6. Perhatikan gambar di bawah ini, jika resultan ketiga buah vektor adalah 5 N, besarnya vektor P adalah....
a. 20 N atau 15 N
b. 5 N atau 15 N
c. 10 N atau 5 N
d. 12 N atau 10 N
e. 12 N atau 15 N
Pembahasan:
7. Dua buah vektor A dan B memiliki besar yang sama. Jika besar resultan kedua vektor sama dengan vektor A dan B tersebut, maka sudut apit antara kedua vektor tersebut adalah...
a. 30⁰
b. 45⁰
c. 120⁰
d. 150⁰
e. 60⁰
Atau
Besar selisih dan jumlah dua buah vektor adalah sama, sudut apitnya adalah ...
a. 0⁰
b. 60⁰
c. 90⁰
d. 120⁰
e. 180⁰
Pembahasan:
8. Ditentukan 2 buah vektor yang besarnya sama dengan F. Bila perbandingan antara besar jumlah dan selisih kedua vektor sama dengan , maka sudut yang dibentuk kedua vektor itu adalah ...
, maka sudut yang dibentuk kedua vektor itu adalah ...
a. 0⁰
b. 30⁰
c. 45⁰
d. 60⁰
e. 90⁰
Pembahasan:
9. Tiga buah gaya pada gambar masing-masing besarnya F1 = 8 N, F2 = 4 N, dan F3 = 8 N tersusun seperti pada gambar berikut. Resultan ketiga gaya ini adalah....
a. 4 N
b. 12 N
c. 8 N
N
d. 8 + 8 N
+ 8 N
e. 8 + 12 N
+ 12 N
Pembahasan:
Materi vektor merupakan materi yang sulit dipahami oleh siswa jika tidak dijelaskan materi matematika trigonometri terlebih dahulu. Materi trigonometri terkait dengan notasi sin 𝞪, cos 𝞪, dan tan 𝞪 yang sangat terkait dalam penjabaran vektor pada koordinat Cartesius pada arah sumbu x dan sumbu y. Agar lebih cepat dipahami siswa, sebaiknya siswa dijelaskan konsep sin 𝞪 dan cos 𝞪.
Jika siswa sudah memahami konsep mata, maka kita mengubah konsep tersebut dengan mengganti mata menjadi 𝞪 (alpha), 𝞫 (beta), 𝞬 (gamma) atau simbol lain.
Jadi sisi di depan mata atau simbol dinamakan depan.
sisi yang menghadap sudut siku-siku dinamakan miring
sisi antara mata atau simbol dengan sudut siku-siku dinamakan samping
Kemudian dijelaskan konsep trigonometri tentang sin 𝞪, cos 𝞪, dan tan 𝞪.

Kemudian siswa dijelaskan dan diberi contoh dengan cara memberi nilai pada setiap variabel baik x, y, dan r.
Jika dinyatakan dalam bentuk sin 𝛂, cos 𝛂, dan tan 𝛂 diperoleh:
Pada materi vektor, sisi miring r dianggap sebagai vektor utama. Jika r mewakili dari vektor gaya, maka ditulis dengan notasi "F", jika r mewakili dari vektor kecepatan, maka ditulis dengan notasi "v", dan sesuai dengan besaran yang diwakilinya.
Tanda garis miring // menunjukkan panjang bagian/sisi atas atau bawah arah horisontal yaitu x memiliki panjang yang sama. Besar panjang x dari rumus cos 𝛂 dan merupakan komponen vektor yang searah sumbu x adalah:
x = r. cos 𝛂
Tanda garis miring /// menunjukkan panjang bagian/sisi kiri atau kanan arah vertikal yaitu y memiliki panjang yang sama. Besar panjang y dari rumus sin 𝛂 dan merupakan komponen vektor yang searah sumbu y adalah:
y = r. sin 𝛂
Selain pemahaman konsep tersebut, siswa dibekali nilai sin 𝞪, cos 𝞪, dan tan 𝞪 dari sudut-sudut istimewa yang biasa digunakan.
Sudut lain yang dipakai sin 37⁰ = 0,6; sin 53⁰ = 0,8; cos 37⁰ = 0,8; dan cos 53⁰ = 0,6.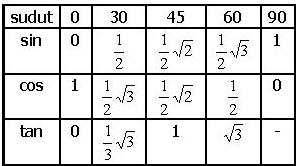 |
| www.wordpress.com |
1. Sebuah Gaya yang Bekerja di Bidang Koordinat Cartesius
1.a. Penguraian Sebuah Gaya di Koordinat Cartesius Kuadran 1
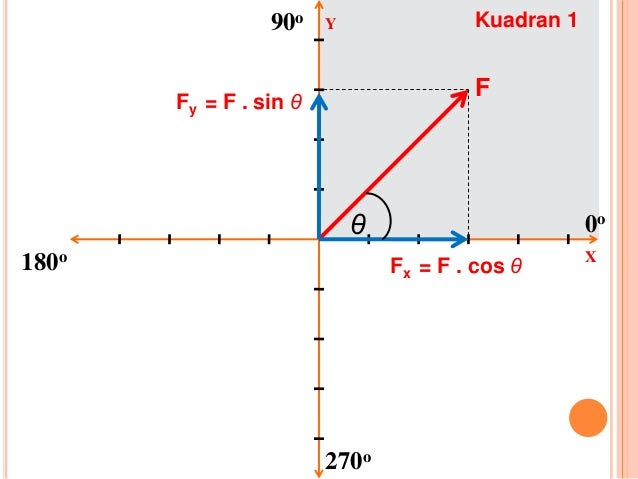 |
| www.slideshare.net |
Misalnya gaya yang bekerja sebesar 10 N dengan sudut sebesar 30⁰ , maka
Fx = F. Cos 𝛉 = 10. Cos 30⁰ = 10. 1/2
Fy = F. Sin 𝛉 = 10. Sin 30⁰ = 10. 1/2= 5 N
1.b. Penguraian Sebuah Gaya di Koordinat Cartesius Kuadran 2
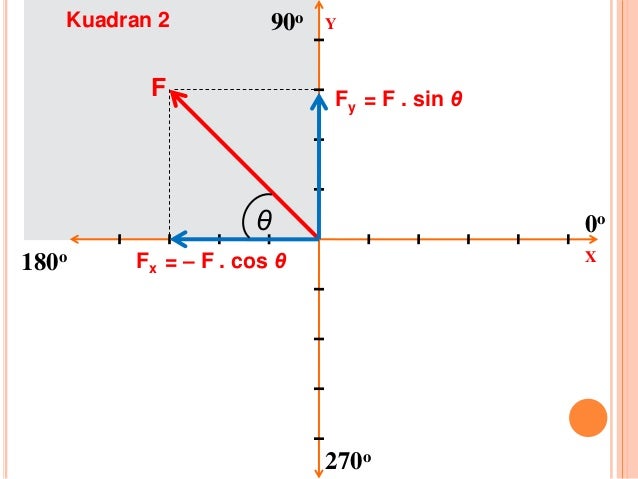 |
| www.slideshare.net |
Misalnya gaya yang bekerja sebesar 40 N dengan sudut sebesar 30⁰ , maka
Fx = F. Cos 𝛉 = 40. Cos 30⁰ = 40. 1/2
Fy = F. Sin 𝛉 = 40. Sin 30⁰ = 40. 1/2= 20 N
1.c. Penguraian Sebuah Gaya di Koordinat Cartesius Kuadran 3
Fx = F. Cos 𝛉 = 60. Cos 30⁰ = 60. 1/2 = 30
= 30 N
N
 |
| www.slideshare.net |
Sebuah vektor gaya yang bekerja pada kuadran 3 menghasilkan penguraian gaya yaitu searah sumbu x negatif sebesar Fx = F. Cos 𝛉 dan searah sumbu y negatif sebesar Fy = F. Sin 𝛉.
Misalnya gaya yang bekerja sebesar 60 N dengan sudut sebesar 30⁰ , maka
Fy = F. Sin 𝛉 = 60. Sin 30⁰ = 60. 1/2= 30 N
1.d. Penguraian Sebuah Gaya di Koordinat Cartesius Kuadran 4
Sebuah vektor gaya yang bekerja pada kuadran 4 menghasilkan penguraian gaya yaitu searah sumbu x positif sebesar Fx = F. Cos 𝛉 dan searah sumbu y negatif sebesar Fy = F. Sin 𝛉.
Misalnya gaya yang bekerja sebesar 50 N dengan sudut sebesar 30⁰ , maka
Fx = F. Cos 𝛉 = 50. Cos 30⁰ = 50. 1/2 = 25
= 25 N
N
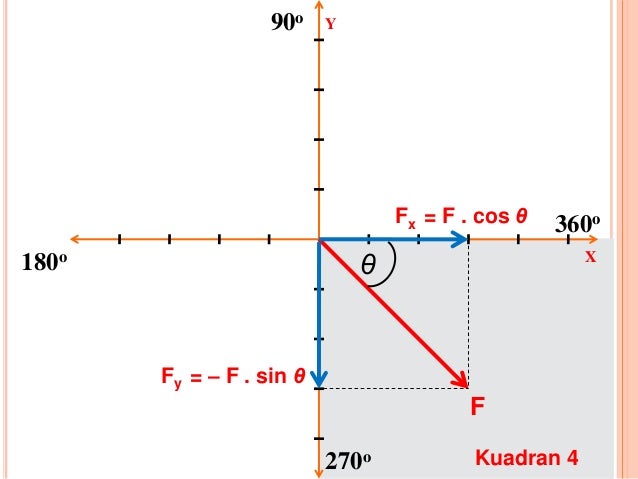 |
| www.slideshare.net |
Misalnya gaya yang bekerja sebesar 50 N dengan sudut sebesar 30⁰ , maka
Fx = F. Cos 𝛉 = 50. Cos 30⁰ = 50. 1/2
Fy = F. Sin 𝛉 = 50. Sin 30⁰ = 50. 1/2= 25 N
1.e. Penguraian Gaya di Koordinat Cartesius dengan Sudut antara Vektor dan Sumbu Y
Jika sudut berada di antara vektor dan sumbu y, maka agar lebih mudah dipahami seperti konsep awal dan tidak mengubah rumus awal serta membuat siswa binggung, harus dicatat adalah sudut yang digunakan yaitu sudut antara vektor dan sumbu x. Sehingga 𝛉 = 90⁰- 30⁰ = 60⁰
1.f. Penguraian Gaya Bekerja yang Searah sumbu x di Koordinat Cartesius
Jika gaya bekerja yang searah dengan sumbu x atau membentuk sudut 0⁰ terhadap sumbu x, misalnya gaya sebesar 20 N, hal ini menunjukkan hanya memiliki komponen Fx = 20 N, sedangkan Fy = 0 N, atau dengan rumus diperoleh:
Fx = F. Cos 𝛉 = 20. Cos 0⁰ = 20. 1 = 20 N
Fy = F. Sin 𝛉 = 20. Sin 0⁰ = 20. 0 = 0 N


Jadi arah resultan gaya sebesar 57⁰ dari sumbu x positif.
2.b. Dua gaya di kuadran 1 dan kuadran 3
Perhatikan grafik berikut!
Tentukan resultan dan arah resultan dari kedua gaya tersebut!
Pembahasan:
Komponen F1 yang searah sumbu x adalah
F1x = F1. Cos 𝛉 = 60. Cos 30⁰ = 60. 1/2 = 30
= 30 N
N
Komponen F1 yang searah sumbu y adalah




Sudut Arah Resultan Gaya:


2.c. Dua gaya di kuadran 3 dan kuadran 4
Tentukan resultan dan arah resultan dari kedua gaya tersebut!
Pembahasan:
Komponen F1 yang searah sumbu x adalah
F1x = F1. Cos 𝛉 = 40. Cos 60⁰ = 40. 1/2= 20 N
Komponen F1 yang searah sumbu y adalah

Resultan dari Jumlah Kedua Vektor:
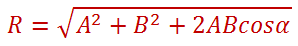
Resultan dari Selisih Kedua Vektor:
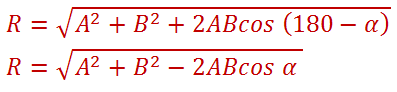
1.g. Penguraian Gaya Bekerja yang Searah sumbu y di Koordinat Cartesius
Jika gaya bekerja yang searah dengan sumbu y atau membentuk sudut 90⁰ terhadap sumbu x, misalnya gaya sebesar 40 N, hal ini menunjukkan hanya memiliki komponen Fx = 0 N, sedangkan Fy = 40 N, atau dengan rumus diperoleh:
Fx = F. Cos 𝛉 = 40. Cos 90⁰ = 40. 0 = 0 N

Sudut Arah Resultan Gaya:
Fy = F. Sin 𝛉 = 40. Sin 90⁰ = 40. 1 = 40 N
2. Dua Gaya bekerja di Koordinat Cartesius




2.a. Dua gaya di kuadran 1 dan kuadran 2
Perhatikan grafik berikut!
Tentukan resultan dan arah resultan dari kedua gaya tersebut!
Pembahasan:
Komponen F1 yang searah sumbu x adalah
F1x = F1. Cos 𝛉 = 40. Cos 30⁰ = 40. 1/2 = 20
= 20 N
N
Komponen F1 yang searah sumbu y adalah

𝚺Fx = (F1x) - (F2x)
𝚺Fx = (20 - 10) N
- 10) N

𝚺Fy = (F1y + F2y) - (0 atau tidak ada gaya ke arah y negatif)
𝚺Fy = (20 + 10 ) N
) N
Resultan Gaya:




Untuk = 1,7
= 1,7

2. Dua Gaya bekerja di Koordinat Cartesius
Rumus-Rumus Fisika yang digunakan dalam penyelesaian dua gaya atau lebih antara lain:
a) Komponen vektor searah sumbu x:
b) Komponen vektor searah sumbu y:
c) Besar Resultan Gaya:
d) Arah Resultan Gaya:
Perhatikan grafik berikut!
Tentukan resultan dan arah resultan dari kedua gaya tersebut!
Pembahasan:
Komponen F1 yang searah sumbu x adalah
F1x = F1. Cos 𝛉 = 40. Cos 30⁰ = 40. 1/2
Komponen F1 yang searah sumbu y adalah
F1y = F1. Sin 𝛉 = 40. Sin 30⁰ = 40. 1/2= 20 N
Komponen F2 yang searah sumbu x adalah
F2x = F2. Cos 𝛉 = 20. Cos 60⁰ = 20. 1/2= 10 N
Komponen F2 yang searah sumbu y adalah
F2y = F2. Sin 𝛉 = 20. Sin 60⁰ = 40. 1/2 = 20
= 20 N
N
F2x = F2. Cos 𝛉 = 20. Cos 60⁰ = 20. 1/2= 10 N
Komponen F2 yang searah sumbu y adalah
F2y = F2. Sin 𝛉 = 20. Sin 60⁰ = 40. 1/2
𝚺Fx = (F1x) - (F2x)
𝚺Fx = (20
𝚺Fy = (F1y + F2y) - (0 atau tidak ada gaya ke arah y negatif)
𝚺Fy = (20 + 10
Resultan Gaya:
Untuk
Sudut Arah Resultan Gaya:
Jadi arah resultan gaya sebesar 57⁰ dari sumbu x positif.
2.b. Dua gaya di kuadran 1 dan kuadran 3
Perhatikan grafik berikut!
Tentukan resultan dan arah resultan dari kedua gaya tersebut!
Pembahasan:
Komponen F1 yang searah sumbu x adalah
F1x = F1. Cos 𝛉 = 60. Cos 30⁰ = 60. 1/2
Komponen F1 yang searah sumbu y adalah
F1y = F1. Sin 𝛉 = 60. Sin 30⁰ = 60. 1/2= 30 N
Komponen F2 yang searah sumbu x adalah
F2x = F2. Cos 𝛉 = 30. Cos 60⁰ = 60. 1/2= 15 N
Komponen F2 yang searah sumbu y adalah
F2y = F2. Sin 𝛉 = 30. Sin 60⁰ = 30. 1/2 = 15
= 15 N
N
𝚺Fx = (F1x) - (F2x)
𝚺Fx = (30 - 15) N
- 15) N

𝚺Fy = (F1y) - (F2y)
𝚺Fy = (30 - 15 ) N
) N
Untuk = 1,7
= 1,7


Resultan Gaya:
𝚺Fx = (30
𝚺Fy = (F1y) - (F2y)
𝚺Fy = (30 - 15
Untuk
Sudut Arah Resultan Gaya:
Jadi arah resultan gaya sebesar 7,125⁰ dari sumbu x positif.
2.c. Dua gaya di kuadran 3 dan kuadran 4
Perhatikan grafik berikut!
Pembahasan:
Komponen F1 yang searah sumbu x adalah
F1x = F1. Cos 𝛉 = 40. Cos 60⁰ = 40. 1/2= 20 N
Komponen F1 yang searah sumbu y adalah
F1y = F1. Sin 𝛉 = 40. Sin 60⁰ = 40. 1/2 = 20
= 20 N
N
Komponen F2 yang searah sumbu x adalah
F2x = F2. Cos 𝛉 = 20. Cos 30⁰ = 20. 1/2 = 10
= 10 N
N
Komponen F2 yang searah sumbu y adalah
F2y = F2. Sin 𝛉 = 20. Sin 30⁰ = 20. 1/2= 10 N
𝚺Fx = (F1x) - (F2x)
𝚺Fx = (20- 10 ) N
) N

𝚺Fy = (0 atau tidak ada serarah sumbu y positif) - (F1y+F2y)
𝚺Fy = - (20 + 10) N
+ 10) N
Untuk = 1,7
= 1,7
𝚺Fx = (20- 10 ) = 20 - 17 = 3N
) = 20 - 17 = 3N
Resultan Gaya:


Sudut Arah Resultan Gaya:

 Jadi arah resultan gaya sebesar -86⁰ dari sumbu x positif atau 86⁰ searah arah jarum jam di kuadran 4.
Jadi arah resultan gaya sebesar -86⁰ dari sumbu x positif atau 86⁰ searah arah jarum jam di kuadran 4.
𝚺Fx = (20- 10
𝚺Fy = (0 atau tidak ada serarah sumbu y positif) - (F1y+F2y)
𝚺Fy = - (20
Untuk
𝚺Fx = (20- 10
𝚺Fy = - (20 + 10) = -(34 + 10) = - 44 N
+ 10) = -(34 + 10) = - 44 N
Resultan Gaya:
Sudut Arah Resultan Gaya:
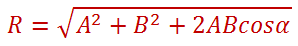
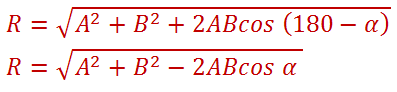
1. Perhatikan vektor gaya di bawah ini!
Jika nilai F = 2 N, nilai komponen vektor pada sumbu x dan sumbu y yang tepat adalah ...
a. Fx = 1 N d. Fx = -1 N
Fy =
b. Fx = 1 N e. Fx =
Fy = -
c. Fx =
Fy = 1 N
Pembahasan:
Fx = F. Cos 𝛉 = 2. Cos 60⁰ = 2. 1/2 = 1 N
2. Perhatikan vektor gaya di bawah ini!
4. Dua buah vektor yang besarnya sama memiliki perbandingan jumlah dan selisih vektor Fy = F. Sin 𝛉 = 2. Sin 60⁰ = 2. 1/2=
N
2. Perhatikan vektor gaya di bawah ini!
Pada gambar diatas, Fy = komponen gaya F pada sumbu Y. Jika Fy = 2 N, komponen gaya pada sumbu X sebesar ... N
a. 2/3 d. 4
d. 4
b. 2 e. 4
e. 4
c. 2
Pembahasan:
Fy = F. Sin 𝛉
2 = F. Sin 60⁰
2 = F. 1/2


3. Kapal yang berlayar di kanal ditarik dengan dua gaya dari sisi kiri dan kanan. Setiap gaya sebesar 1.200 N. Kedua gaya membentuk sudut 45 terhadap arah mendatar. Nilai komponen vektor pada sumbu x di sisi kiri kapal sebesar ... N.
a. 600. d. 1200
b. 600. e. 2.400
c. 1.200
Pembahasan:
c. 2
Pembahasan:
Fy = F. Sin 𝛉
2 = F. Sin 60⁰
2 = F. 1/2
3. Kapal yang berlayar di kanal ditarik dengan dua gaya dari sisi kiri dan kanan. Setiap gaya sebesar 1.200 N. Kedua gaya membentuk sudut 45 terhadap arah mendatar. Nilai komponen vektor pada sumbu x di sisi kiri kapal sebesar ... N.
a. 600. d. 1200
b. 600. e. 2.400
c. 1.200
Pembahasan:
Sudut apit kedua vektor tersebut adalah....
a. 60⁰
b. 30⁰
c. 150⁰
d. 120⁰
e. 45⁰
Pembahasan:
5. Gaya-gaya berikut bekerja pada suatu benda: 7 N ke utara, 20 N berarah 37 dari timur, dan 4 N ke barat. Besar resultan ketiganya adalah.... (sin 37 = 0,6)
a. 5 N
b. 10 N
c. 13 N
d. 22,5 N
e. 25 N
Pembahasan:
6. Perhatikan gambar di bawah ini, jika resultan ketiga buah vektor adalah 5 N, besarnya vektor P adalah....
a. 20 N atau 15 N
b. 5 N atau 15 N
c. 10 N atau 5 N
d. 12 N atau 10 N
e. 12 N atau 15 N
Pembahasan:
7. Dua buah vektor A dan B memiliki besar yang sama. Jika besar resultan kedua vektor sama dengan vektor A dan B tersebut, maka sudut apit antara kedua vektor tersebut adalah...
a. 30⁰
b. 45⁰
c. 120⁰
d. 150⁰
e. 60⁰
Atau
Besar selisih dan jumlah dua buah vektor adalah sama, sudut apitnya adalah ...
a. 0⁰
b. 60⁰
c. 90⁰
d. 120⁰
e. 180⁰
Pembahasan:
8. Ditentukan 2 buah vektor yang besarnya sama dengan F. Bila perbandingan antara besar jumlah dan selisih kedua vektor sama dengan
a. 0⁰
b. 30⁰
c. 45⁰
d. 60⁰
e. 90⁰
Pembahasan:
9. Tiga buah gaya pada gambar masing-masing besarnya F1 = 8 N, F2 = 4 N, dan F3 = 8 N tersusun seperti pada gambar berikut. Resultan ketiga gaya ini adalah....
a. 4 N
b. 12 N
c. 8
d. 8
e. 8
Pembahasan:
10. Dua vektor perpindahan memiliki nilai 8 m dan 12 m. Jika kedua vektor saling mengapit sudut 60 , selisih duavektor tersebut sebesar ... m.
Pembahasan:
11. Dua vektor P dan Q besarnya 40 dan 20 satuan. Jika sudut antara kedua vektor tersebut sebesar 60 , nilai P - Q adalah ...
Pembahasan:
Bus pariwisata





























terimakasih, sangat membantu
ReplyDeleteTerima kasih kembali, semoga bermanfaat.
Deletesemoga lebih banyak karya dan sukses
ReplyDelete